近似算法在Apache火花:HyperLogLog和分位数
介绍
Apache火花是快,但应用,如初步数据勘探需要更快,愿意牺牲一些更快的结果的准确性。1.6版本以来,引发实现近似算法对一些常见的任务:计数设置不同的元素的数目,发现如果一个元素属于一个集合,计算一些基本统计信息大量的数字。从集体,尤金Zhulenev已经博客在这些页面使用的近似计算的广告业务。
下面的算法实现了DataFrames和数据集并提交到Apache火花的分支- 2.0,所以他们可以在Apache 2.0火花Python, R, Scala:
- approxCountDistinct:返回一个估计的数量不同的元素
- approxQuantile:返回数值数据的近似百分位数
研究人员考察了这种算法很长一段时间。火花努力实现近似算法确定的(他们不依赖于随机数字工作)和已被证明的理论误差范围:对于每一个算法,用户可以指定一个目标错误绑定,结果是保证在这个绑定,要么完全(确定性误差范围)或非常高的信心(概率误差范围内)。此外,重要的是,该算法适用于用例的财富的火花社区。
在这个博客中,我们目前的实现细节approxCountDistinct和approxQuantile算法和展示其实现砖的笔记本。
近似数不同的元素
在古代,想象居鲁士大帝巴比伦,波斯皇帝,刚刚完成了所有他的帝国的人口普查,想知道有多少不同的名字被使用在他的整个帝国,和他把维齐尔的任务。维齐尔知道主人是不耐烦,希望答案快,即使只是一个近似。
有一个问题,尽管;一些名字如大流士,Atusa或Ardumanish非常受欢迎,经常出现在人口普查记录。简单的计算有多少人生活在帝国会给一个贫穷的回答,皇帝不会被愚弄。
然而,做了一些现代和深奥的数学知识。他组装的所有宫殿的仆人,说:“仆人,你们每个人将粘土平板从人口普查记录。对于每个名字刻在平板电脑,你将第一个三个字母的名称,称为l1, l2和l3,和计算以下数量:
N = l1 + 31 * l2 + 961 * l3例如,对于大流士(D = 3 = 0, R = 17),你会得到N = 16340。
这将给你一个号码为每一个平板电脑的名称。对于每一个数字,你会数一数的零这个数字。在侯赛因(N = 17739)的情况下,这会给你没有零。后你们每个人,每个名字在他或她的平板电脑,你会召开,你会告诉我什么是你观察到最大数量的零。现在继续伟大的匆忙,没有计算错误,以免你要忍受我的忿怒!”
早上结束时,一个仆人回来了,并说他们已经找到了一个有四个零,这是他们最大的所有观察到的所有人口普查记录。维齐尔然后宣布他的主人,他的主人人口约为1.3 * 10 ^ 4 = 13000个不同的名字。皇帝非常深刻的印象,他问大臣他如何完成这一壮举。维齐尔的说出一个词:“hyper-log-log”。
HyperLogLog算法(及其变体HyperLogLog + +实现火花)依赖于聪明的观察:如果这个数字是一致通过一系列传播,然后不同元素可以近似的计数最多的前导零二进制表示的数字。例如,如果我们观察一个数字的位数二进制形式的形式0…(k) 01…1,那么我们可以估计有2 ^ k元素的顺序。这是一个非常粗糙的估计,但它可以精炼到伟大的草图算法精度。
从上面的示例大臣和他的仆人,该算法不需要进行洗牌,只是地图(每个服务适用于平板电脑)和组合(仆人能使双并决定哪一个最大数量,直到只有一个仆人)。没有需要移动数据,只有小每个数据块的统计信息,这使得它非常有用在大型数据集设置如火花。
现在,在现代,这种技术情况如何工作,数据集在哪里更大当仆人取代火花集群?我们认为是25数百万在线评论的数据集从一个在线零售供应商,我们出发去近似的数量客户背后的这些评论。因为客户写多个评论,这是一个适合近似的计算。
这里是如何让用户的一个近似计算PySpark,在1%的真实价值和有高概率:
用户:DataFrame(用户:字符串)
用户。选择(approxCountDistinct(“用户”,rsd = 0.01)),告诉()
该地块(图1)显示不同的客户不同的数量误差。正如预期的那样,答案变得越来越精确要求误差减小。
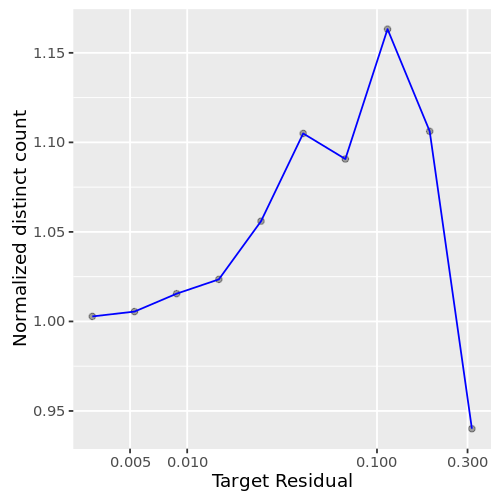
需要多长时间来计算?在上面的分析中,该地块(图2)介绍了运行时间的近似计算精度要求。错误超过1%,运行时间是一分钟分数计算确切的答案。为精确的答案,然而,运行时间增加非常快,最好是直接计算确切的答案。
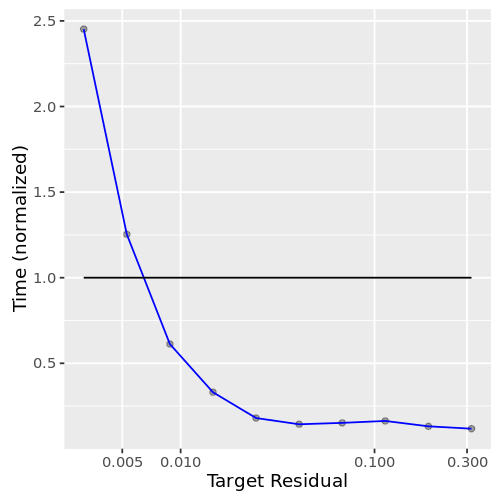
作为结论,使用approxCountDistinct时,你应该记住以下几点:
- 当请求错误的结果是高(> 1%),近似的计算是非常快,并返回结果的一小部分的成本计算准确的结果。事实上,或多或少相同的性能目标误差为20%或1%。
- 更高的精度,该算法撞了墙,开始花费更多的时间比精确计数。
近似分位数
分位数(百分位数)在很多情况下是有用的。例如,当web服务执行大量的请求,重要的是要有请求的延迟等性能的见解。更普遍的是,当面对大量的数字,一个是经常感兴趣的一些聚合信息如均值、方差,最小值,最大值,百分位数。同时,是有用的只有极端分位数:前1%,0.1%,0.01%,等等。
火花实现一个健壮的、著名的算法起源于流数据库社区。像HyperLogLog,计算一些数据在每个节点,然后聚合引发司机。当前算法在火花贸易可以调节精度与计算时间和内存。基于相同的例子,我们看每个评论文本的长度。大多数评论者表达他们的意见在几句话,但有些客户是多产的作家:最长的评论数据集是超过1500个单词,虽然有几千词评论语法上有不同程度的自由。
我们这里情节(图3)中位数的长度审查(50百分位)以及更极端的百分位数。这个图表表明,很少有很长的评论,大部分都是低于300个字符。
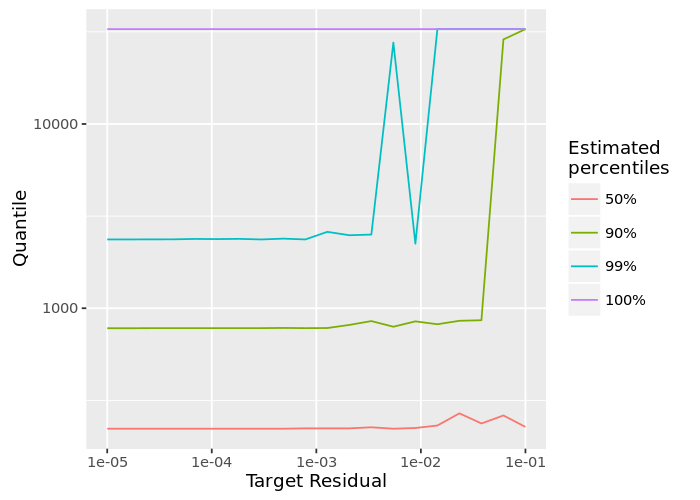
近似的行为分位数HyperLogLog一样:当要求粗略估计在几个百分点的确切答案,该算法精确计算要快得多(图4)。更精确的答案,一个精确的计算是必要的。
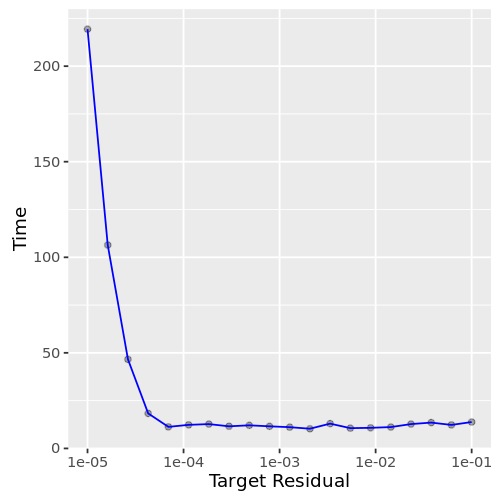
结论
我们展示的实现细节approxCountDistinct和approxQuantile算法。虽然引发操作非常快,有时探索性数据应用需要更快的结果牺牲为代价的准确性。这两个算法实现更快的执行。
Apache 2.0火花将包括一些先进的近似算法更快的结果。用户可以选择之间快速、不精确的答案,更慢,确切的答案。还有其他一些近似算法你想看到吗?让我们知道。
现在这些算法实现数据砖笔记本。自己试试,注册一个帐户与砖在这里。


